Concepts

Kinematics

1. Vector: a quantity that has both magnitude(amount) and direction. Ex: 35 miles(magnitude) west(direction)
2. Scalar: a quantity that has only magnitude. Ex: 25 mph.
3. Distance vs. Displacement
   1. Distance (scalar) is how far something moves and it includes the path travelled. Ex: 3 meters
      1. Distance can NOT be negative, no matter where the object goes. This is because distance, being a scalar has no directional value
   2. Displacement (vector) is the straight-line distance from where the object started to where it ended. Ex: 2 Meters 36 degrees
      1. Displacement is the change in position of an object. Δx = xf − xi
      2. Displacement, being a vector, can be negative. Ex: going backwards.

2D Kinematics

There isn’t much different about 2D motion. Simply “copy and paste” the equations change the variables and a few rules. But there are many important concepts to understand: THE X AND Y DIRECTION ARE SEPARATE (diff. values EXCEPT TIME) ax=0, so vx is constant. t is the same in both Y and X directions-good variable to solve for \(a_y = 10\) (downward)

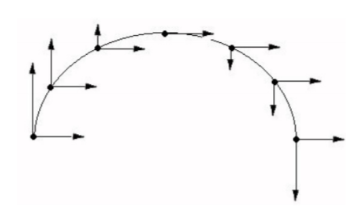
If given initial velocity at an angle(resultant), separate it into its components:

\[V_x = V*cosθ ; V_y = V*sinθ\]

• Ground-to-ground: path is symmetrical, so at the max height: Vy=0, and t = ½ * the total time.
• Horizontal to ground: \(V_{oy} = 0\)
• Elevated ground: path is symetrical until the object goes under initial height
• Note: \(a_y\) can be negative or positive, but you MUST BE CONSISTENT, so the sign of Δy should be the same.

---

Position(x) Time(t) graph:

• Slope: \(\frac{\Delta x}{\Delta t} = v\)
• Area between the equation and the x/time axis: NOTHING (there is nothing before position - \(x*t=nothing\))

  Velocity(v) Time(t) graph:

• Slope: \(\frac{\Delta v}{\Delta t} = \frac{\Delta x}{\frac{\Delta t}{\Delta t}} = acceleration(a)\)
• Area: \(\Delta v * \Delta t = \frac{\Delta x}{\Delta t} * t = \Delta x = displacement(x)\)

  Average [value] = \(\frac{\Delta value}{\Delta t}\)

• Ex: average velocity = \(\frac{x - x_0}{t - t_0}\)